Une sélection de résultats

Reconstruction du champ magnétique coronal

Dans ce paragraphe, je vais décrire de manière très accessible et peu technique une thématique de recherche à laquelle je me suis intéressée il y a plus d'une dizaine d'années (en collaboration avec Tahar Amari). Il n'est pas exclu que nous reprenons ce travail très prochainement (fortes chances de rechute!!).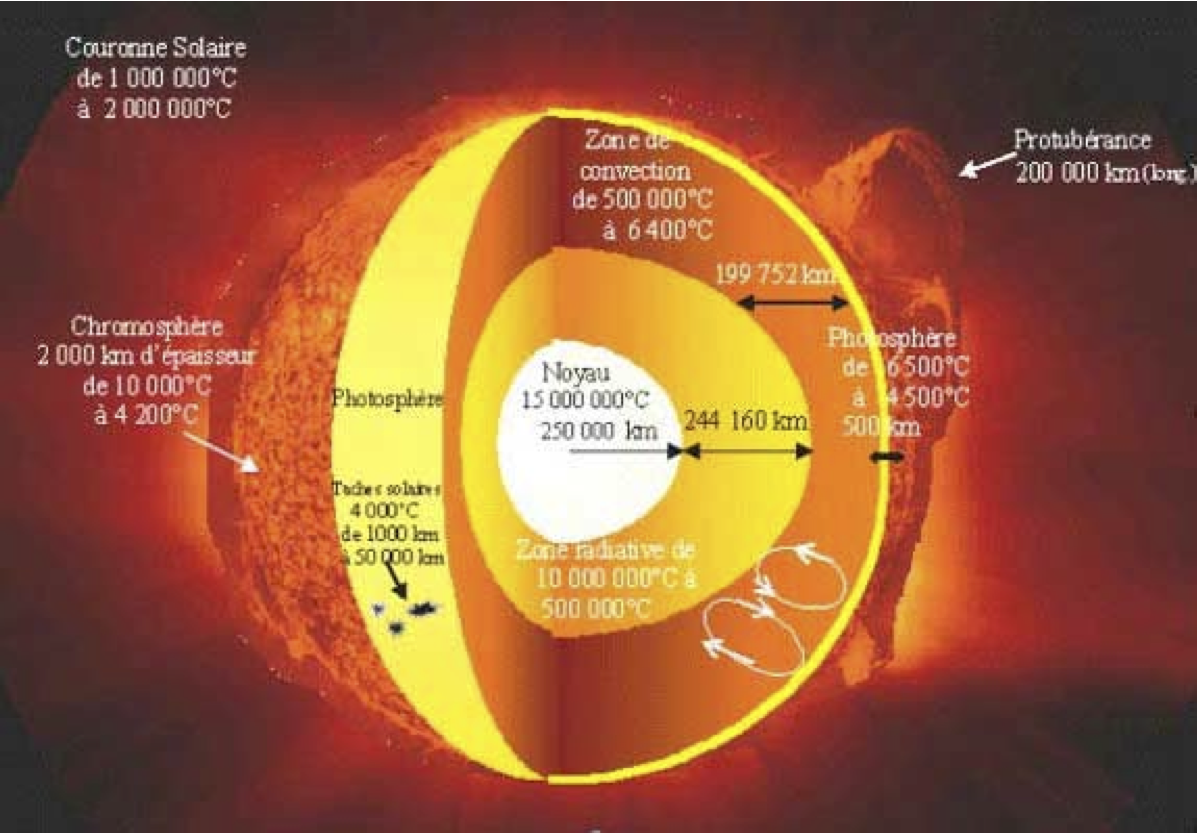

Il s'agit d'une application des mathématiques en astrophysique, notamment en physique en solaires. Ici je présenterai la thématique plus que nos résultats scientifique.

Selon nos connaissances actuelle, l'univers dans lequel nous vivons contient au minimum une centaine de milliards de Galaxies. Un cortège de centaines de milliard d'étoiles erre au sein de notre galaxie, La Voie Lactée. Le Soleil est l'une de ces étoiles. Une étoile une étoile simple; ses grandeurs caractéristiques (âge, taille, température,...etc) sont en effet proches de la moyenne de la plupart des étoiles.

Pourtant, pour nous humains, le soleil est unique en son genre. Car, il est non seulement un facteur fondamental de l'existence de la vie sur notre planète, mais aussi la seule étoile qui s'offre réellement à la curiosité des astronomes et des astrophysiciens, là, pas trop loin, à une distance idéale.

Une simple observation du Soleil montre qu'il est le théatre d'un ensemble extraordinaire de phénomènes où rentrent en jeu pratiquement toutes les forces connues de la nature. Pour les physiciens, c'est un laboratoire providentiel grandeur nature, impossible à réaliser sur Terre. Il leur permet de vérifier jusqu'aux théories les plus acquises de la physique fondamentale.

Regardé de plus près, le Soleil est une boule compacte, gazeuse et très chaude. Elle est animée d'une rotation différentielle, et se maintient par l'effet de sa propre gravitation. Les modèles d'aujourd'hui s'accordent tous sur le fait qu'elle comporte plusieurs couches aux caractéristiques très différentes. Au centre il y a un noyau, petit mais très massif, dans lequel se produit un nombre incalculable de réactions et qui est source de la quasi-totalité de l'énergie. Le noyau est enveloppé dans deux couches successives très épaisses: une couche radiative intermédiaire et une couche de convection. Le tout est entouré d'une surface très mince et extrêmement brillante qu'on appelle la photosphère. Elle sépare de manière nette l'intérieur du soleil de son atmosphère. Ensuite, à partir de la photosphère, on distingue d'abord une première couche, moins dense et plus transparente appelée la chromosphère. Elle forme une transition progressive entre la surface du soleil et la couronne. La couronne est la zone très peu dense qui s'étend jusqu'à l'espace interstellaire, bien au delà de la Terre. Lorsqu'on observe le soleil dans la lumière blanche c'est essentiellement le rayonnement de la photosphère qu'on voit. C'est uniquement durant les éclipses totales du soleil, ou en occultant le disque solaire par un coronographe, qu'on peut voir la couronne sous forme d'un halo de lumière blanche, qui l'entoure en s'étalant à des distances lointaines.

Historiquement, l'observation du soleil remonte aux civilisations et aux temps les plus anciens. Aujourd'hui, il est placé sous surveillance ininterrompue par des astronomes du monde entier; des téléscopes fixés à des endroits stratégiques (ou, pour éviter l'absorption et la turbulence de l'atmosphère terrestre, embarqués sur des satellites paparazzi) épient et enregistrent de manière continuelle son comportement. Les observations consistent principalement à analyser le spectre du rayonnement électromagnétique solaire, des ondes radioélectriques jusqu'aux rayons X et $\gamma$. C'est la spectroscopie; elle permet de déterminer la structure de la surface et l'atmosphère solaire en localisant les pics spectraux du rayonnement, dus aux transitions atomiques, signatures des éléments émetteurs ou absorbants. En outre, en utilisant certains effets connus de la physique, tels que l'effet Doppler et l'effet Zeeman, la spectroscopie permet aussi de mesurer des grandeurs physiques importantes du plasma, telles que la température, la vitesse et le champ magnétique, et cela essentiellement au niveau de la photosphère, qui est beaucoup plus dense et paradoxalement beaucoup moins chaude que les régions inférieures de la couronne.

La photosphère est donc la véritable surface du soleil; à partir d'elle la brillance et la densité chutent très rapidement. Plus important encore est que la photosphère délimite d'un point de vue qualitatif la partie intérieure, où l'effet mécanique (c'est-à-dire les mouvements du plasma) l'emporte, de la partie extérieure dominée complètement par le champ magnétique. Ce champ magnétique joue un rôle fondamental dans la formation de la plupart des structures observées au dessus de la photopshère; régions actives, protubérances, taches solaires,...etc. En outre, on le suppose aussi responsable des phénomènes de chauffage coronal, des protubérances, du vent solaire et de certaines manifestations très violentes telles que les éruptions et les éjections coronales de masses. Sur Terre, lors des périodes d'activité solaire maximale, ces éruptions causent des orages magnétiques qui perturbent remarquablement les liaisions radioélectriques, téléphoniques, voire même électriques dans certaines zones, et augmentent aussi les flux de particules dans les aurores boréales aux deux pôles. Comprendre la morphologie et les propriétés des structures stables (ou quasi-stables) repérées par les observations et reconstituer les mécanismes de l'apparition des éruptions est en effet le défi majeur de la physique solaire actuelle.
$$ \def\j{{\bf j}} \def\B{{\bf B}} \def\E{{\bf E}} \def\div{{\rm div}\,} \def\rot{{\bf rot}\,} \def\B{{\bf B}\,} \def\e{{\bf e}\,} \def\v{{\bf v}} \def\qq{{\bf q}} \def\zero{{\bf 0}} \def\n{{\bf n}} \def\C{{\mathbb{C}}} \def\N{{\mathbb{N}}} \def\R{\mathbb{R}} \def\F{{\bf F}} \def\g{{\bf g}} \def\om{\Omega} \def\x{{\bf x}} \def\s{{\bf s}} \def\b{{\bf b}} \def\R{\mathbb{R}} \def\X{{\bf X}} \def\pt{\partial} \def\dps{\displaystyle} $$ Modélisation du champ magnétique coronal

La physique de l'atmosphère solaire est celle qui décrit l'intéraction d'un plasma avec un champ magnétique. D'un point de vue macroscopique, les équations utilisées pour décrire cette interaction sont appelées les équations de la magnétohydrodynamique (MHD). Ces équations sont un couplage des équations de Navier-Stokes instationnaire (régissant les aspects mécaniques) et les équations de Maxwell (régissant le champ électromagnétique). Elles forment un système non-linéaire reliant les grandeurs physiques scalaires et vectorielles caractérisant le plasma; la densité $\rho$, la pression $p$, la température $T$, la vitesse $\v$, la densité du courant électrique $\j$, le champ électrique $\E$ et le champ magnétique $\B$. Si on suppose que le plasma est continu, isotrope et en équilibre thermodynamique, ces équations de la MHD s'écrivent:

• Les équations de Maxwell
  $$ \begin{array}{l} \rot \B = \mu \j + \dps{ \frac{1}{c^2}\frac{\partial \E}{\partial t}}, \\ \div\B = 0, \\ \rot \E = -\dps{ \frac{\partial \B}{\partial t}}, \\ \div \E = \frac{\rho^*}{\epsilon}, \end{array} $$ où $\rho^*$ est la densité de charge, $\mu$ la perméabilité magnétique, $\epsilon$ la permitivité du milieu et $c$ la vitesse de la lumière.
  
  
• La loi d'Ohm
  Dans ce contexte, cette loi s'écrit: $$ \j = \sigma (\E+ \v \times \B), $$ $\sigma$ étant la conductivité électrique.
  
  
• Equation de la conservation de masse
  $$ \frac{\partial \rho}{\partial t} + \div ( \rho \v ) = 0 . $$
  
• L'équation du mouvement
  $$ \rho \frac{d\v}{dt} = - \nabla p + \j \times \B + \F , $$ où $\F = \F_g + \F_v $ est la somme de la force de gravité $\F_g = -\rho \g(r) \e_r $ et de la force de viscoscité $\F_v = \rho \nu (\Delta \v + \frac{1}{3}\nabla(\div \v))$.
  
  
• L'équation d'état des gaz parfaits
  $$ p = \frac{R}{\mu_0} \rho T , $$ avec $R$ la constante des gaz et $\mu_0$ la masse moyenne des particules (l'unité étant la masse d'un proton par exemple).
  
  
• L'équation de l'énergie
  $$ \frac{\rho^\gamma}{\gamma - 1} \frac{d}{dt}(\frac{p}{\rho^\gamma}) = -\div \qq - L_r + \frac{j^2}{\sigma} = \rho \epsilon + H_v + H_w , $$ où :
  $\qq = -\kappa \nabla T$ le flux de chaleur ($\kappa$ la conduction thermique).
  $L_r = \div q_r = -\div(\kappa_r \nabla T)$; la radiation nette.
  $\epsilon \; : \;$ l'énergie nucléaire générée par unité de masse.
  $H_v = \rho \nu\dps{(\frac{1}{2} e_{ij} e_{ij} - \frac{2}{3} (\div \v)^2)}$: le taux de dissipation visqueuse ($\dps{ e_{ij} = \frac{\partial v_i}{\partial x_j} - \frac{\partial v_j}{\partial x_i}}$).
  $H_w$ : terme de chaleur ondulatoire.
  

En outre, on suppose communément que les variations électromagnétiques ne sont pas relativistes; il en découle que le terme $\dps{\frac{1}{c^2}\frac{\partial \E}{\partial t}}$ est négligeable devant les autres termes de l'équation, et on a donc: $$ \rot \B = \mu \j. $$ Maintenant, en éliminant le champ $\E$ et le courant $\j$ dans les équations ci-dessus on obtient l'équation d'induction: $$ \frac{\partial \B}{\partial t} = \rot (\v \times \B) - \rot(\eta \rot \B), $$ où $\eta = \dps{ \frac{1}{\mu \sigma}}$ est la coefficient de diffusion magnétique. Dans le plasma sous la photosphère, la vitesse $\v$ est déterminée par d'autres forces. L'équation d'induction décrit alors l'évolution du champ magnétique induit par le mouvement du plasma.
A partir de la photosphère, cette relation de cause à effet s'inverse et c'est le champ magnétique qui domine toutes les autres forces au niveau de la chromosphère et la couronne. Dans cette zone, la vitesse du plasma peut être supposée négligeable devant la vitesse du son, la vitesse d'Alfvén et la vitesse de Chute libre gravitationnelle. En plus, la dissipation résistive se fait souvent de manière très lente car le coefficient $\eta$ est très petit. L'équation d'induction implique alors que le champ magnétique évolue lentement et peut être supposé décrire une série d'équilibres statiques dont la lente évolution est due essentiellement aux déplacements des pieds des lignes de force, entrainés au niveau de la photosphère par les mouvements convectifs sous-photosphériques.

Par ailleurs, les éruptions solaires, dont l'origine est située dans les zones les plus brillantes des régions actives, semblent être l'effet d'une évolution rapide à partir d'une configuration d'équilibre où le plasma est confiné dans une topologie complexe du champ magnétique.

Les équilibres du champ magnétique coronal sont gouvernés par des équations déduites directement des équations de la MHD considérées dans le cas statique ($\partial . /\partial t = 0$). Ainsi, en omettant les termes dûs à la vitesse, supposée négligeable dans le couronne, l'équation du mouvement, qui exprime l'équilibre des forces, s'écrit: $$ \j \times \B -\nabla p + \F_g = \zero. \;\;\;\;\;\;\;\;\;\;(EQ) $$ En outre, le terme de gravitation aussi bien que le gradient de la pression peuvent être négligés dans cette équation. En effet, concernant le terme de pression, les observations montrent que le nombre $\beta$ du plasma, rapport de la pression thermique et de la pression magnétique $$ \beta = \frac{2 \mu p_0}{B_0^2}, $$ est très petit devant 1 au niveau de la couronne. L'équation $(EQ)$ devient alors $$ \j \times \B = 0, $$ ce qui veut dire que pour assurer l'équilibre, la seule force dominante, c'est-à-dire la force de Lorentz, doit être nulle. En conclusion, compte tenu des deux premières équations de Maxwell, le champ magnétique $\B$ doit vérifier le système $$ \left\{ \begin{array}{rcl} \rot \B \times \B &=& \zero ,\\ \div \B &=& 0. \end{array} \right.\;\;\;\;\;\;\;\;\;\;(BT) $$ Lorsqu'il y a équilibre, le champ magnétique au-dessus de la photosphère est donc un champ force-free ou de Beltrami.

Au stade actuel des choses, l'unique observation vraiment précise du champ magnétique provient de la photosphère, couche plus dense et moins chaude que la couronne où le champ reste très difficile à mesurer.

L'étude mathématique du problème non-linéaire $(BT)$ s'est avérée compliquée. Il en va de même de l'approximation de la solution.

Notre contribution consiste en plusieurs points

• Etude théorique champs de Beltrami (voir la rubrique correspondante ou cliquer ici pour plus de détails)
• Mise en place de méthodes d'approximation des solutions d'équilibres (cliquer ici pour plus de détails)
• Utilisation de données réelles mesurés comme conditions aux limites
• Proposition et implémentation de schémas numériques pour les problèmes d'évolution (MHD).